1 - Définitions relatives aux risques naturels
2 - Définition économique du risque
3 - Evaluation de l'aléa
4 - Des bases mathématiques pour la combinatoire des facteurs de risque
5 - Notions d'interactions, de synergie, de compensation et d'auto-pénalisation

1 - Définitions relatives aux risques naturels :

    Ce que l'on appelle dans le langage courant le risque correspond formellement à la notion d'aléa.

    D'après Brugnot, délégué national aux risques naturels au Cemagref (1998) le risque peut se définir comme le croisement entre deux dimensions : aléa x vulnérabilité.

    L'aléa est le phénomène physique aléatoire. L'aléa implique une notion de probabilité. La notion de risque s'oppose à la notion de certitude. Certains problèmes environnementaux se posent en terme de risque (la contamination des eaux par les pesticides ou par le phosphore provenant du rusisellement sur les sols). D'autres problèmes environnementaux, comme celui de la pollution du réseau hydrographique par les nitrates, ne se posent pas en termes de risque (quand les bilans d'azote sont fortement excédentaires la pollution est une certitude).

    La vulnérabilité est le pendant de l'aléa en termes économiques ou en terme de vies humaines de l'aléa en question.
    Exemples : risque lié aux avalanches, risque lié aux tornades ou typhons tropicaux.

    Dans le langage courant en Français, quand on parle de risque de quelque chose, on parle en fait de l'aléa.
    Exemples :     risque d'avalanche = aléa avalanche
                         risque de typhon = aléa typhon.

    Le risque est, comme nous le verrons plus tard, pluri-factoriel. Ces facteurs peuvent être de différentes natures ; certains facteurs sont stationnels, d'autres sont non stationnels.

    Pour les facteurs stationnels on peut utiliser la notion d'exposition (exposition au risque d'avalanche par exemple). On parle par exemple relativement au risque lié aux avalanches de situation exposée : telle situation (ensemble d'habitations) est dans une situation exposée ; cette situation est exposée à l'aléa avalanche : ceci signifie alors que dans cette situation la probabilité d'avalanche est assez élevée. Notons que si cette situation est construite, elle devient une situation à forte vulnérabilité.

2 - Définition économique du risque :

    En économie on appelle risque l'espérance mathématique des coûts :
                        r(s) = S p_j * c_j                                                                                                                       (1)

    avec         j : classe de gravité (attention, le terme gravité est ici utilisé dans le sens courant et non dans celui de gravité d'un facteur) et
                    p_j : probabilité d'un événement de gravité j donnée et de coût c_j

    2.1. Exemple du risque lié à la conduite automobile :

    On peut illustrer simplement cette définition utilisée dans le domaine de l'assurance avec l'exemple du risque inhérent à la conduite d'un véhicule automobile : pour chaque catégorie socio-professionnelle (CSP), les compagnies d'assurance déterminent la probabilité annuelle d'occurrence d'un accident par classe de coût (moins de 1000 F, entre 1000 et 2000 F, etc...). Ces probabilités permettent de calculer le risque annuel d'un accident automobile par CSP et donc de calculer le montant de la prime d'assurance.

  2.2. Exemple du risque sismique :

    Prenons un deuxième exemple : celui du risque sismique dans un site donné, par exemple, celui de la faille de San Andreas en Californie. Les séismes sont classés avec l'échelle d'intensité de Mercalli ou par l'échelle MSK ou EMS92. On utilise aussi l'échelle de magnitude de Richter. L'énergie dispensée pendant un séisme est une fonction exponentielle de l'échelle de Richter. Dans un site donné, on peut connaître assez bien la probabilité d'occurrence des séismes de faible intensité. Par contre, on connaît mal la probabilité des séismes de forte intensité, tout simplement parce que leur probabilité d'occurrence est extrêmement faible et qu'il s'agit d'un type d'événement qui est très rarement intervenu voire jamais. On construit donc la courbe de probabilité d'occurrence des séismes, partiellement sur des données expérimentales et partiellement sur de l'extrapolation. De même, on construit la courbe des coûts et on peut évaluer le risque.

  2.3. Exemple du risque de crues :

    Cet exemple se présente d'une manière assez analogue à celui du risque sismique. Dans un site donné, on peut connaître assez bien la probabilité d'occurrence des crues de faible intensité. Par contre, on connaît mal la probabilité des crues de forte intensité, tout simplement parce que leur probabilité d'occurrence est extrêmement faible et qu'il s'agit d'un type d'événement qui est très rarement intervenu voire jamais. On construit donc la courbe de probabilité d'occurrence des crues, partiellement sur des données expérimentales et partiellement sur de l'extrapolation.

    D'autres solutions sont aussi utilisées. Par exemple, la méthode AGREGE du Cemagref où l'on construit la première partie de la courbe de probabilités à partir de données de crues observées et où l'on construit la deuxième partie de la courbe à partir des données météorologiques sur les probabilités d'occurrence des averses de très forte intensité. Cette méthode est fondée sur l'hypothèse qu'au delà d'un certain seuil la fonction de production pluie-crue est égale à 1 et sur le fait que les séries de données météorologiques sont bien souvent plus longues et plus complètes que les séries de données sur les crues.

  2.4. Transposition de la définition économique du risque dans le domaine de l'environnement :

    Dans le domaine de l'environnement, on peut faire l'hypothèse - au moins dans un premier temps - que les coûts sont proportionnels aux flux de produits polluants.

    Prenons l'exemple du risque de flux de phosphore vers le réseau hydrographique.
Supposons que le coût d'un tel flux soit proportionnel au niveau de perte :
            c_j = k * q_j
            avec qj perte en phosphore par hectare.
On a alors : r(s) / k = S p_j * q_j
            S p_j * q_j est une estimation moyenne des pertes annuelles en phosphore.

    L'application de cette méthode d'évaluation des pertes en phosphore au cas de la Bretagne conduit aux résultats suivants : les pertes en phosphore seraient de 2 à 3 kg/ha/an dans l'Est, Nord-Est de la Bretagne et entre 0,5 et 1 kg/ha/an dans l'Ouest, Sud-Ouest de la Bretagne.

    Mais il n'est pas certain que ces chiffres respectent rigoureusement la méthode et concrètement ces chiffres ne semblent pas prendre en compte les événements rares à faible probabilité d'occurrence. Quand on écrit que les pertes moyennes en phosphore peuvent descendre dans l'Ouest, Sud-Ouest à 0,5 kg/ha/an, ce chiffre ne semble pas intégrer des flux importants de plusieurs dizaines de kg/ha mais n'occurrant qu'avec une très faible probabilité annuelle (comprise entre 0,01 et 0,1).

    Ceci signifierait que la moyenne serait en fait mal évaluée et qu'elle n'intègre pas les événements exceptionnels et graves...

3 - Evaluation de l'aléa :

    La plupart du temps le risque-aléa est pluri ou multifactoriel : plusieurs facteurs de risque concourent à un risque-aléa donné.

    On distinguera n facteurs de risque-aléa élémentaires ou partiels (i = 1 , n) qui concourent à un risque-aléa global donné.

  3.1. Notations :

    Soit s une situation : s peut être une parcelle (dans une problématique de risque pesticide) ou un point de l'espace (x,y) (dans une problématique de risque d'érosion).
    Soit f _i(s), le facteur de risque-aléa i pour la situation s ; f _i(s) est soit une fonction continue (par exemple dans le cas de la pente) ou une fonction discrète (dans le cas du type de sol, ou du type d'occupation du sol).
    Soit r[f _i(s)], le risque-aléa élémentaire lié au facteur i de la situation s. Souvent r[f _i(s)] est la "note de risque" du facteur i. Dans certains cas, en particulier dans le domaine de la logique floue, on prendra r[f _i(s)], appartenant à l'intervalle [0,1].

Pour simplifier la notation, on peut noter r_i(s) le risque-aléa élémentaire lié au facteur i de la situations.

  3.2. Exemples simples ou simplistes (naïfs) de méthodes de combinaison des facteurs de risque :

    Citons quelques exemples simples ou simplistes de méthodes servant à évaluer le risque-aléa global à partir des risques-aléa élémentaires ou partiels :
    Avec une méthode additive, le risque-aléa global est égal à r(s) = S r_i(s)                                (2)
    Dans une telle méthode additive, les n facteurs de risque-aléa élémentaires ou partiels sont considérés de gravité égale, à moins que l'étendue des valeurs des ri(s) des n facteurs de risque-aléa partiels ne cache en fait des gravités différentes.

    Avec une méthode dite combinatoire r(s) = S g_i * r_i(s)                                                         (3)
    avec g_i poids du facteur i.
    g_i est encore appelé gravité du facteur i et
    r_i(s) est l'exposition de la situation s au facteur de risque-aléa i.

    Mais la plupart du temps, on ne connaît pas les gravités des n facteurs de risque-aléa partiels.

  3.3. La technique dite des « arbres de décision » :

    Une technique souvent appelée improprement des "arbres de décision" est souvent ou parfois utilisée. Cette appellation est impropre dans le sens où elle laisse supposer que cette technique permettrait de prendre une décision ou que l'arbre générerait une décision.

    En fait dans l'utilisation de cette technique, il y a deux phases : (1) la phase de construction de l'arbre, (2) la phase de décision, c'est-à-dire de classement et de définition du risque par dire d'expert. La première phase n'est en rien une phase de décision mais une phase qui permet de distinguer des situations les unes des autres en utilisant un arbre. En fait on devrait appeler cette phase : phase de distinction. Les arbres utilisés sont souvent des arbres binaires ; il s'agira alors d'arbres dichotomiques. Mais on peut utiliser aussi des arbres ternaires ou n-aires.

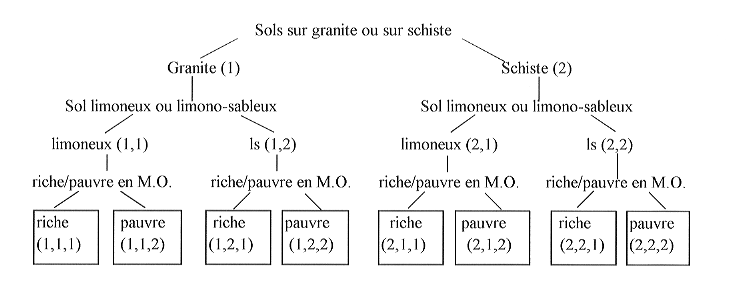
    A chaque niveau de l'arbre une question permet de distinguer des situations entre elles. Voyons un exemple :

    Dans cet exemple, huit situations sont distinguées. Elles ne sont en rien classées relativement à un risque. Elles sont classées entre elles selon une méthode dichotomique. Mais deux experts consultés sur une question différente vont classer ces huit situations de façon différente.

    Le premier expert consulté sur le risque d'érosion va par exemple classer ces huit situations de la façon suivante (du plus fort au plus faible) :
(2.1.2) > (1.1.2) > (2.2.2) > (1.2.2) > (2.1.1) > (1.1.1) > (2.2.1) > (1.2.1)

    Le deuxième expert consulté sur le risque de contamination des pesticides par ruissellement va par exemple classer ces huit situations de la façon suivante (du plus fort au plus faible) :
(2.1.2) > (1.2.2) > (2.2.2) > (1.1.2) > (2.1.1) > (1.2.1) > (2.2.1) > (1.1.1)

    Cet exemple naïf illustre simplement le fait que le classement en terme de risque dépend du risque étudié et que ce classement n'a aucune raison d'être le même que le classement issu de la construction de l'arbre.

    On est évidemment tenté de hiérarchiser les facteurs (par exemple du plus important vers le moins important) pour faire apparaître les clefs de construction de l'arbre. Si l'on reprend l'exemple du le risque de contamination des pesticides par ruissellement, l'expert va classer les 3 facteurs de la façon suivante : (1) teneur en matière organique du sol, (2) texture du sol, (3) nature géologique et on notera d la modalité défavorable et 0 la modalité non défavorable :

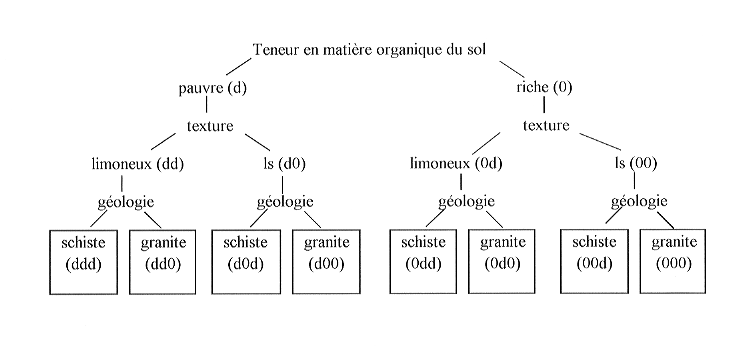
    On peut avoir l'illusion à l'observation de cet arbre que les huit situations qui sont distinguées seraient classées de la situation la plus à risque (ddd) à la moins à risque (000). Ceci n'est qu'illusion, on s'en convaincra en observant l'adjacente entre la situation (d00) et la situation (0dd). Même si le premier facteur est hiérarchiquement plus important que les deux autres, il n'est pas certain que la présence simultanée du deuxième et du troisième facteur dans leur modalité défavorable (0dd) ne fasse pas de ce cas une situation plus à risque que (d00). Ceci pose le problème de la combinatoire des facteurs de risque et des lois d'agrégation qui seront développées plus loin.

    En appliquant les règles qui découlent de la hiérarchie entre facteurs le classement se présente de la façon suivante :
(ddd) > (dd0) > (d0d) > (d00) ? (0dd) > (0d0) > (00d) > (000)

        Avec deux solutions :
                a) (ddd) > (dd0) > (d0d) > (d00) > (0dd) > (0d0) > (00d) > (000)
                b) (ddd) > (dd0) > (d0d) > (0dd) > (d00) > (0d0) > (00d) > (000)

    Dans le cas des arbres binaires ou dichotomiques, comme dans l'exemple précédent le nombre de situations distinguées est de 2n, n étant le nombre de clefs utilisées pour construire l'arbre. A partir de n >= 5, les meilleurs experts sont dans l'impossibilité de classer les situations entre elles en terme de risque.

    De même dans le cas des arbres ternaires, le nombre de situations distinguées est de 3n, n étant le nombre de clefs utilisées pour construire l'arbre. Et à partir de n >= 3, les meilleurs experts sont dans l'impossibilité de classer les situations entre elles en terme de risque.

    Pour contourner cette difficulté on utilise souvent la technique des arbres simplifiés : par exemple, on considérera que toutes les situations, où le premier facteur est dans la modalité défavorable, sont plus défavorables quelque n'importe quelle autre combinaison des facteurs. Dans le cas d'un arbre binaire à cinq clefs, on aura alors 17 situations au lieu de 32 situations:
        (dxxxx) (0dddd) (0ddd0) (0dd0d) (0dd00) (0d0dd) (0d0d0) (0d00d) (0d000) (00ddd) (00dd0) (00d0d) (00d00) (000dd) (000d0) (0000d) (00000)
            et par application de la règle énoncée plus haut des arbres simplifiés, on pose :
        (dxxxx) > (0dddd) (0ddd0) (0dd0d) (0dd00) (0d0dd) (0d0d0) (0d00d) (0d000) (00ddd) (00dd0) (00d0d) (00d00) (000dd) (000d0) (0000d) (00000)

    En appliquant les règles qui découlent de la hiérarchie entre facteurs le classement des seize situations « de droite » peut-être présenté de la façon suivante :
       (0dddd) > (0ddd0) > (0dd0d) > (0dd00) ? (0d0dd) > (0d0d0) > (0d00d) > (0d000) ? (00ddd) > (00dd0) > (00d0d) > (00d00) ? (000dd) > (000d0) > (0000d) > (00000)

    On en déduirait les relations suivantes :
        (dxxxx) > (0dddd) > (0ddd0) > (0dd0d) > (0dd00) ? (0d0dd) > (0d0d0) > (0d00d) > (0d000) ? (00ddd) > (00dd0) > (00d0d) > (00d00) ? (000dd) > (000d0) > (0000d) > (00000)

    Dans un tel cas d'arbre simplifié, il faut évidemment faire appel à un expert pour classer les 16 situations autres que (dxxxx), car ces 16 situations ne sont évidemment pas classées relativement au risque étudié.

    Mais de toute façon cette procédure de simplification de l'arbre ne peut être que rejetée car la première inégalité est très certainement inexacte car il est certain que parmi les seize situations qui se retrouvent groupées sous (dxxxx) il y a des situations dont le risque est inférieur à certaines des seize situations de droite de l'arbre. Par exemple (d0000) a très certainement un risque inférieur à (0dddd) dans bon nombre de cas.

   Cette solution technique des arbres dits simplifiés doit donc être considérée la plupart du temps comme non satisfaisante.

    Un autre défaut fréquemment observé dans l'utilisation des arbres est celui des arbres déséquilibrés. On reprendra pour cela le premier exemple d'arbre qui est un exemple d'arbre déséquilibré. On fera les hypothèses suivantes : les schistes au sens large représentent 70% d'un territoire, les granites 30%, les sols limoneux 90% des schistes et 60 % des granites, les sols riches en matière organique 50 % du territoire indépendamment des autres facteurs :

    Dans cet exemple naïf, on observe qu'une situation donnée peut avoir une occurrence plus de cinq fois plus grande qu'une autre. Dans l'exemple réel de l'application d'un tel arbre sur la Région Bretagne, on trouvera une situation parmi huit recouvrant à elle seule plus de 40 % du territoire.

    Ces arbres déséquilibrés ne conviennent évidemment pas bien pour distinguer des situations entre elles puisque les situations distinguées ont des probabilités d'occurrence trop dissemblables les unes des autres.

    Pour toutes ces raisons la technique des arbres de décision devra être manipulée avec d'infimes précautions et on ne peut pas en conseiller l'utilisation sans un appui technique solide en dehors du cas où le nombre de situations distinguées entre elles est faible (significativement moins de 20).
 

  3.4. La question du croisement entre gravité et risque partiel :

    Pour estimer le risque-aléa partiel attribuable au facteur i, l'un des problèmes est de croiser l'exposition et la gravité (l'exposition au facteur i de la situation s étudiée et la gravité du facteur i). Plusieurs méthodes peuvent être utilisées pour cela.

    Citons quelques exemples symétriques :
        1 - g_i * r_i(s)
        2 - min [  g_i , r_i(s) ]
        3 - 1/2 * [  g_i + r_i(s) ]
        4 - max [ g_i, r_i(s) ]

    Mais on peut faire la remarque suivante : a priori le rôle joué par gravité et exposition n'est pas symétrique. Naïvement, on remarquera, en effet que le risque n'est sans doute pas le même si la gravité d'un facteur est de 0,8 et l'exposition à ce facteur de risque de 0,3 et si la gravité d'un facteur est de 0,3 et l'exposition à ce facteur de risque de 0,8. On pourrait donc être tenté d'adopter une méthode de croisement non symétrique, c'est-à-dire faisant appel à une écriture non symétrique en g_i et r_i(s).

    Mais on peut faire la remarque supplémentaire suivante : de toute façon le rôle de gi et de ri(s)ne sont pas symétriques car il y a une contrainte sur les gravités :
        S g_i = 1
alors qu'il n'y a pas de contrainte sur les risque élémentaires ri(s).

    Ce fait - présence d'une contrainte versus absence de contrainte - est peut-être suffisant pour assurer cette non symétrie sans qu'il soit nécessaire de faire appel à un opérateur non symétrique en g_i et r_i(s).

4 - Des bases mathématiques pour la combinatoire des facteurs de risque :

  4.1. Une méthode hiérarchique :

    La méthode SIRIS proposée par Vaillant et al., 1995 et utilisée ultérieurement par Aurousseau et al. 1998 est une méthode hiérarchique qui ne nécessite pas la définition des gravités des facteurs mais seulement leur classement hiérarchique du plus grave au moins grave. Elle met en fait en oeuvre des règles (auto-pénalisation, etc...) qui ne sont pas très évidentes à expliciter.

    Cette méthode met en oeuvre un ensemble de règles d'agrégation qui ont été explicitées par Vaillant et al. La publication laisse planer un doute entre deux hypothèses. Heureusement les exemples d'utilisation fournis par Vaillant et al. permettent de lever ce doute. Squividant a sur la base de la publication de Vaillant écrit en langage C le code de la méthode SIRIS jusqu'à un maximum de 10 facteurs et de 5 modalités par facteur.

    Les règles d'agrégation inclues dans la méthode SIRIS constituent une solution pour tous les cas ambigus de combinatoires de modalités comme dans les exemples que nous avons vus plus haut : (d00) ? (0dd) ou encore (0dd00) ? (0d0dd) ou (0d000) ? (00ddd) ou (00d00) ? (000dd)

    Nous allons présenter le principe de la méthode S.I.R.I.S. La méthode S.I.R.I.S. est une méthode par pénalisation, de type hiérarchique (la pénalité de doo est toujours supérieure à celle de odo, elle même supérieure à celle de ood). De même moo > omo >oom.

    Les modalités sont toujours classées dans le même ordre : "o", "m", "d". Dans le cas de facteurs à deux modalités; elles sont notées "o" et "d". Dans le cas de facteurs à trois modalités, elles sont notées : "o", "m", "d".

    Deux autres modalités notées "md" et "2d" sont considérées dans le cas où deux facteurs à trois modalités ont le même niveau hiérarchique. Ce cas sera explicité plus loin.

    La première règle est la règle d'interaction. Les valeurs des pénalités attribuées aux différentes modalités (sauf pour "o" qui se voit toujours attribuer la pénalité nulle) dépendent de la situation des classes précédentes (des facteurs de risque hiérarchiquement plus importants). En effet, lorsque la situation s'aggrave dans la classe (n), la pénalité attribuée à une modalité donnée de la classe (n+1) augmente.

    On commence par attribuer la pénalité 2 à la modalité "d" du premier bloc de la dernière classe, c'est-à-dire de la classe hiérarchiquement la moins importante (On appelle bloc un fragment de colonne contenant la succession des différents niveaux hiérarchique d'un facteur).

    Puis, lorsque dans la classe précédente, la modalité passe de "o" à "d", on incrémente la pénalité attribuée à "d" dans la dernière classe d'une unité, etc. On a donc une première série d'incrémentations due aux facteurs hiérarchiquement les plus importants.

    Nous allons illustrer l'application de cette règle de l'interaction sur un exemple à 3 facteurs ayant chacun 3 modalités.

    On pourra pour mieux comprendre la notion d'interaction se reporter au paragraphe 6 à la fin de ce document. Et pour illustrer sur un exemple l'effet exact de l'interaction nous allons construire le tableau correspondant à une méthode hiérarchique comme la méthode S.I.R.I.S. mais sans interaction, à la différence de la méthode S.I.R.I.S.

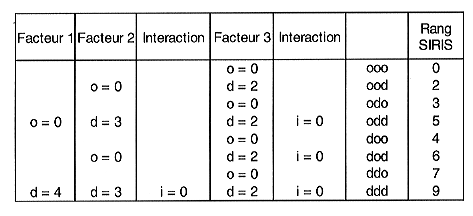
    Construisons maintenant, avec la méthode S.I.R.I.S., le tableau correspondant à trois facteurs avec chacun trois modalités (o, m, d).
    On fixe à 2 la pénalité de la modalité "d" du 3eme facteur (ex 1).
    Quand le facteur 2 passe à la modalité "m" puis "d", on incrémente de 1 la pénalité "d" du 3eme facteur (ex 2 et 3).
    Quand le facteur 1 passe à la modalité "m" puis "d", on incrémente de 1 la pénalité "d" du 3eme facteur (ex 4 et 5).
    Quand pour la modalité "m" du facteur 1, le facteur 2 passe à la modalité "m" puis "d", on incrémente de 1 la pénalité "d" du 3eme facteur (ex 6 et 7).

    Quand toutes les pénalités des modalités "d" du dernier facteur sont fixées, on fixe la plus forte pénalité "d" de facteur précédent en incrémentant la pénalité "d" de 1 et ainsi de suite.

    On décrémente les pénalités "d" des premiers facteurs en appliquant la règle précédente de façon inverse.

    La deuxième règle est la règle de dissymétrie. Cela concerne l'attribution de la pénalité à la modalité "m". On a m = E(d/2) (partie entière de d/2). donc m=d/2 si d est pair et m = (d -1)/2 si d est impair. Cette dissymétrie a une limitation : la pénalité attribuée à "m" doit rester supérieure à la plus haute pénalité attribuée à "m" pour le facteur suivant.

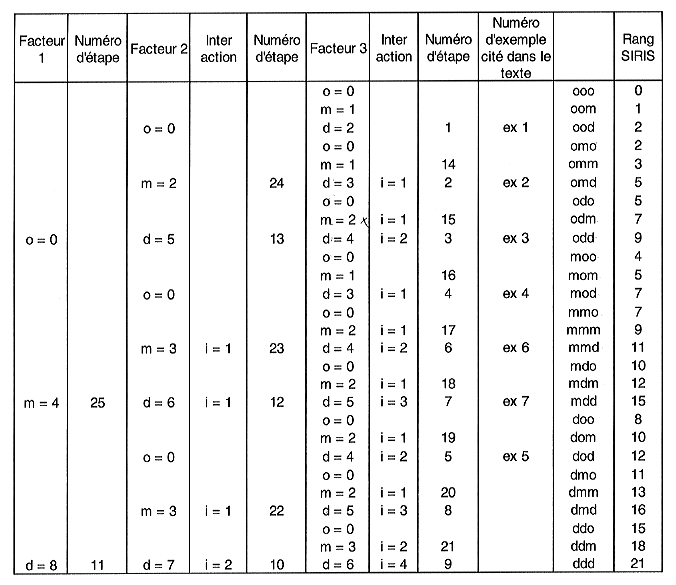
    On pourrait là aussi, à titre d'illustration construire un tableau correspondant à une méthode hiérarchique comme la méthode S.I.R.I.S. mais sans interaction, à la différence de la méthode S.I.R.I.S.

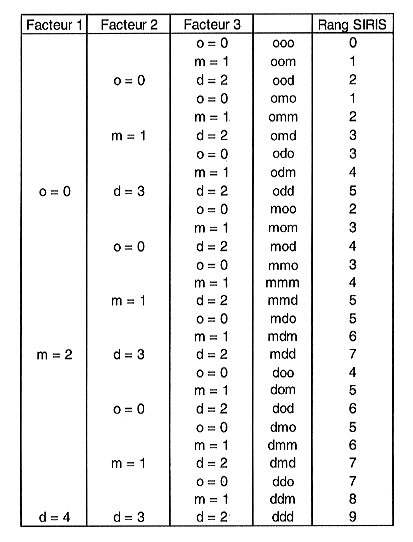
    Compte tenu de la règle de la dissymétrie, on a dans ce tableau m(F₂) = m(F₁) = 1. Pour éviter cette situation qui pourrait être considérée comme un biais (puisque contradictoire avec la règle de la hiérarchie), on pourrait construire un autre tableau avec m(F₂) = 2, d(F₂) = 4, m(F₁) = 3, d(F₁) = 6.

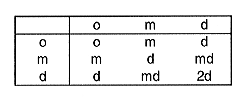
    Lorsque deux variables (à trois modalités chacune) appartiennent à une même classe, on obtient cinq niveaux dont deux niveaux nouveaux notés "md" et "2d". Ils correspondent respectivement à l'intersection d'un niveau "m" et d'un niveau "d" et de deux niveaux de type "d". Dans ce cas "md" a pour pénalité la somme des pénalités de "m" et "d" et "2d" a pour pénalité le double de celle de "d". Le résultat est présenté dans le tableau suivant :

  4.2. Intersection et Union d'ensemble flous :

    Considérons un risque à deux facteurs F₁ et F₂,
            le sous ensemble E₁ des situations à risque relativement au facteur F₁,
            le sous ensemble E₁^Cdes situations non à risque relativement au facteur F₁,
            le sous ensemble E₂ des situations à risque relativement au facteur F₂,
            le sous ensemble E₂^C des situations non à risque relativement au facteur F₂,
            s une situation a :
            r₁(s) ou r(E₁) comme degré d'appartenance au sous ensemble E₁,
            1 - r₁(s) comme degré d'appartenance au sous ensemble E₁^C,
            r₂(s) ou r(E₂) comme degré d'appartenance au sous ensemble E₂,
            1 - r₂(s) comme degré d'appartenance au sous ensemble E₂^C

Première attitude : on considère qu'une situation est à risque si
        la situation est à risque relativement au facteur F₁
                                        ET
        la situation est à risque relativement au facteur F₂
        le sous ensemble des situations à risque est E₁ I E₂ intersection des ensembles E₁ et E₂
        le degré d'appartenance à E₁ IE₂ est : r(E₁ IE₂) <= min ( r(E₁) , r(E₂) )

Deuxième attitude : on considère qu'une situation est à risque si
        la situation est à risque relativement au facteur F₁
                                        OU
        la situation est à risque relativement au facteur F₂
        le sous ensemble des situations à risque est E₁U E₂ union des ensembles E₁ et E₂
        le degré d'appartenance à E₁ U E₂ est : r(E₁ U E₂) >= max ( r(E₁) , r(E₂) )

Troisième attitude : on considère qu'une situation est à risque quelque part entre :
        la première attitude où :
        la situation est à risque relativement au facteur F₁
                                        ET
        la situation est à risque relativement au facteur F₂
et
        la deuxième attitude où :
        la situation est à risque relativement au facteur F₁
                                        OU
        la situation est à risque relativement au facteur F₂
        le sous ensemble des situations à risque R est inclus entre E1 I E2 et E1 U E2,
        le degré d'appartenance à R est r(s) :
        r(E1 I E) <= r(s) <= r(E1 U E2)

    Pour cela, on peut suivre la proposition de l'opérateur hybride de Zymmerman et Zysno (1983) fondée sur les opérateurs d'intersection I et d'union U :
        r(s) = r(E₁ I E)^g. r(E₁ U E₂)^1-g , avec 0 < g< 1         (5)

    Cet opérateur est associatif et permet donc de passer de 2 facteurs à n facteurs de risque, si les opérateurs de conjonction et de disjonction utilisés sont eux-mêmes associatifs.

    L'autre question est celle du choix des opérateurs d'intersection et d'union :
    On peut prendre les opérateurs de Kleene (min et max) mais alors le risque global ne dépend que du plus petit risque partiel et du plus grand mais il ne dépend pas des risques partiels intermédiaires.

    D'où la proposition des opérateurs d'intersection et d'union de Yager :
       r( I ) = 1 - min ( 1 , [ S ( 1 - r _i (s))^w ]^{1 /w}                     (6)
       r( U ) = min ( 1 , [ S  r _i (s)^w ]^{1 /w})                               (7)

       Dans le cas où 0 <= ri(s) <= 1, alors les opérateurs de Yager s'écrivent :
        r( I ) = 1 - [ S ( 1 - r _i (s))^w ]^{1 /w}                                             (8)
       r( U ) = [ S  r _i (s)^w ]^{1 /w}                                                             (9)

    Les opérateurs de Zymmerman et Zysno et de Yager sont des opérateurs qui ont été proposés par une analyse fonctionnelle. Ces opérateurs présentent certaines bonnes propriétés mathématiques (comme l'associativité par exemple).

    Opérateurs de Yager pondérés :

    Si on admet comme dans &3.4. que la contrainte S gi = 1 suffit pour assurer la non symétrie entre gi et ri(s) et que l'on peut donc utiliser une formule symétrique en gi et ri(s), on pourrait alors utiliser l'opérateur « * » comme opérateur symétrique de croisement, d'où :
         r( I ) = 1 - [ S ( 1 - g_i *r_i(s))^w ]^{1 /w}                                    (10)
         r( U ) = [ S ( g_i * r_i(s))^w ]^{1 /w}                                       (11)

    Et en prenant la demi somme comme opérateur de combinaison entre gravité et risque partiel on aurait alors :
        r( I ) = 1 - [ S ( 1 - 0,5*( g_i *r_i(s)))^w ]^{1 /w}                       (12)
        r( U ) = [ S ( 0,5^{w  *} (g_i + r_i(s))^w )]^{1 /w}                        (13)

    On peut alors introduire ces deux écritures dans un opérateur hybride de Zymmerman et Zysno
        r(s) = { 1 - [  S ( 1 - 0,5*( g_i *r_i(s)))^w ]^{1 /w}} ^g * { [  S ( 0,5^{w  *} (g_i  +  r_i(s))^w ]^{1 /w}}^{1 - g}

    Opérateurs d'agrégation :

    Citons l'opérateur de la moyenne proposé par Douaire et Saby pour évaluer le risque d'érosion :
        r(s) =  [ S  g_i * (r_i(s))^w ]^{1 /w}                                       (14)

5 - Notions d'interactions, de synergie, de compensation et d'auto-pénalisation :

    Ces notions ont pour objectif de décrire les propriétés des interactions entre facteurs

    Pour illustrer ces notions mettons nous dans le cas de l'équation (3) où le risque partiel peut s'écrire comme le produit de la gravité d'un facteur par le risque élémentaire et où le risque global est égal à la somme des risques partiels :
        r(s) = S g_i * r_ei(s) = S r_pi(s)

    On dit qu'avec ces opérateurs, il n'y a pas d'interaction entre facteurs de risque.

   Par contre on appellera i l'interaction entre le facteur F₁ et le facteur F₂ si le risque r(s) peut s'écrire :
        r(s) = r_p1(s) + r_p2(s) + i(s)
        avec r_p1(s) et r_p2(s) les risques partiels relatifs aux facteurs F₁ et F₂.

  Synergie :

    Typiquement, on a une interaction synergique si i(s) > 0

  Définition maximaliste :
        si r_e1(s) = r_e2(s) et quelque soit la valeur de r_e1(s) ou r_e2(s), alors r(s) > r_e1(s)
        Avec cette définition la synergie entre 2 facteurs s'observe quelques soit la valeur de r_e1(s) ou r_e2(s)

    Exemple : r_e1(s) = r_e2(s) = 0,3
    Prenons aussi g₁ = 0,3 et g₂ = 0,7
    si r(s) > 0,3 alors r(s) peut s'écrire r(s) = r_p1(s) + r_p2(s) + i(s) avec i(s) > 0

  Autre définition :
            si r_e1(s) = r_e2(s) et si r_e1(s) = r_e2(s) > 0,5 , alors r(s) > r_e1(s)
            Avec cette définition la synergie entre 2 facteurs s'observe uniquement si r_e1(s) et r_e2(s) ont une valeur élevée (par exemple > 0,5).

    Exemple : r_e1(s) = r_e2(s) = 0,6
    Prenons aussi g₁ = 0,3 et g₂ = 0,7
    si r(s) > 0,6 alors r(s) peut s'écrire r(s) = r_p1(s) + r_p2(s) + i(s) avec i(s) > 0

    Définition moins drastique :
            r(s) augmente plus vite en fonction de r_e1(s) quand r_e2(s) est grand plutôt que quand r_e2(s) est petit.

    Cette définition semble cohérente avec la définition de l'auto-pénalisation donnée par Vaillant et al. 1995 et on peut vérifier dans le tableau Siris3.sdc que la méthode S.I.R.I.S. met bien en oeuvre des mécanismes d'interaction positive synergique.

  Compensation :

            Si r_p1(s) est grand et si r_p2(s) est petit, typiquement, on a une interaction de type compensatoire si i(s) < -r_p2(s)
            et alors r(s) < r_p1(s)
            (le facteur de risque 2 compense en partie la forte valeur du facteur de risque 1)

    Tableau construit dans l'hypothèse où rp1(s) > rp2(s) et présentant les différentes valeurs possible de l'interaction entre deux facteurs de risque.

    On remarquera que les opérateurs de Kleene Min et Max mettent en oeuvre des mécanismes d'interaction négative.
   On choisira donc l'opérateur de combinaison de facteurs de risque selon les propriétés que l'on souhaite voir respecter par cet opérateur.

Index