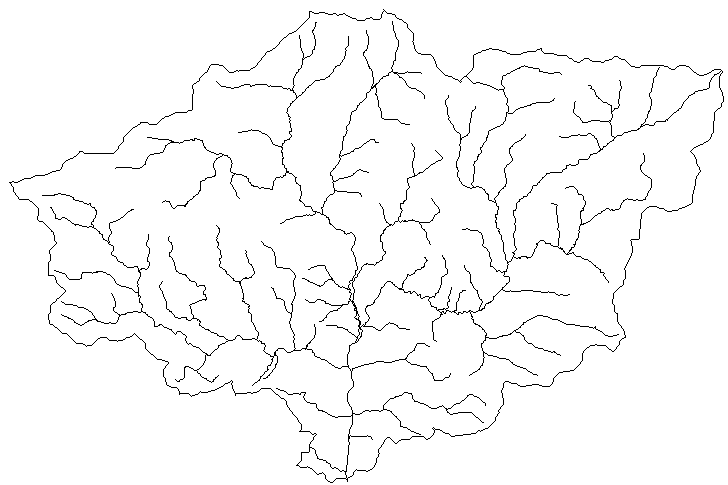
Fig. 1 - n-ary tree structure of a natural drainage pattern (example taken
from upstream section of the the Aulne river basin, Brittany).Figure
1 en 2 dimension (70k)
Pierre Aurousseau, Professor at E.N.S.A.R.
and Hervé Squividant, Information Technology Engineer
Laboratoire de Spatialisation Numérique, E.N.S.A.R.,
65, rue de Saint Brieuc,
35042 Rennes cedex, France
Key words : tree structure, graph structure, digital elevation model, topology, topographic index
Short title : Tree and graph structures in DEM
A certain number of geographical entities display structures that can
be readily represented as trees or graphs. In the general area of Digital
Elevation Model (DEM) applications, particularly regarding the uses of
such models in hydrology, the drainage pattern is a good example of a geographical
system that have a natural organization in terms of trees or graphs. Most
drainage patterns unaffected by human activities exhibit a binary or ternary
tree structure (Fig. 1).

Fig. 1 - n-ary tree structure of a natural drainage pattern (example taken
from upstream section of the the Aulne river basin, Brittany).Figure
1 en 2 dimension (70k)
After anthropic modifications of hydrological systems (e.g. construction
of canals, etc.), the drainage pattern acquires in many cases a graph-like
structure (Fig. 2).
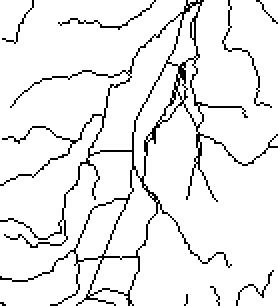
Fig. 2 - Planar graph structure of an artificially modified drainage system
(upper Rhine valley, extracted from Digital Chart of the World and imported
in a 500 m grid size DEM of western Europe).
It is also known that trees and graphs can be use to handle relations which are no longer physical but which represent abstract links between objects. The use of the trees and graphs presented here is of interest in the management of drainage networks. In this study, a drainage network is defined as the set of water flow paths that can be modelled by means of a DEM. Two types of drainage network may be envisaged : monodirectional and multidirectional (Wolock and McCabe 1995).
Use of Digital Elevation models to model water flow pathways in different landscapes
For a number of landscapes developed on ancient massifs composed of compact rocks with low permeability, water circulation is seen to be essentially surficial. There are no deep groundwater bodies and aquifers are always located near the surface. This type of situation occurs for geological terrains comprising shales, sandstones, quartzites and granites, as observed in the Armorican Massif of northwest France. A large proportion of the water passing through the river basin is circulating within a thin layer of soil and unconsolidated, fragmented or fissured material. The soil profile itself has a thickness ranging from a few tens of centimetres to two metres at the most, whereas loose weathered material may attain a thickness of several metres. Beneath this, the fragmented or fissured bedrock extends over a thickness of a few metres. It is possible to estimate that more than 90% of the water volume circulating in the river basin is actually present in a zone of loose, fragmented or fissured material less than 25 m thick. As a result, with cartographic representations at scales greater than 1:25,000, the thickness of the material in which the water is circulating can be assumed to be infinitesimally small. The movement of waters across the terrain can thus be modelled by taking the slope of the topographic surface as the main factor driving the hydrological cycle.
2. Methods
2.1. Construction of a n-ary drainage tree
Monodirectional drainage model
In a monodirectional drainage model, a grid cell of the DEM is assumed
to drain the entire volume of water from its catchment towards the immediately
adjacent cell with the lowest topographic elevation (Fig. 3). In a general
way, a monodirectional drainage model is equivalent to a field of flow
vectors (Fig. 4) where each cell of the Digital Elevation Model has a vector
showing the direction of drainage. A Freeman code may be used to indicate
the drainage direction calculated for each grid cell. The following step
in data processing consists of identifying the drainage outlets.
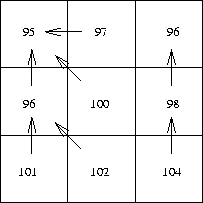
Fig. 3 - Example of a monodirectional drainage model.

Fig. 4 - Drainage model (flow vector field)
Outlet search procedure
The outlets correspond either to grid cells with zero
elevation or cells situated at the edge of the Digital Elevation Model.
Alternatively, an outlet may also occur at an enclosed site (i.e. surrounded
by eight cells that are all higher than the central cell), in which case
it is usually known as a drainage anomaly(Fig. 5).

Fig. 5 - Example of a monodirectional drainage model in the vicinity of
a drainage anomaly.
This type of situation is not normally encountered in nature except
under special environmental conditions: karst areas, closed drainage systems
and moraines. Normally, outlets are sorted and stored in order of increasing
elevation. Outlets of the same elevation are ranked according to their
order of occurrence during a search run through the Digital Elevation Model.
After location of the outlets, the next step is to construct a drainage
tree for each identified outlet(Fig. 6).
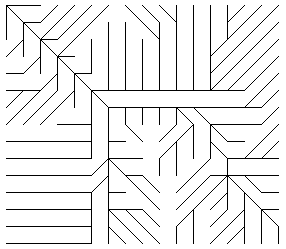
Fig. 6 - A monodirectional drainage network.
The drainage tree is thus a unique geographical entity that enables a description to be made of the entire water flow pattern contributing to a given outlet.
Correction of drainage anomalies
Because of the size of the DEMs under consideration (containing from one million to several million grid cells), it is out of the question to employ manual solutions for the correction of drainage anomalies. For DEMs with widely spaced grid steps (of the order of 250 m and 500 m), the number of anomalies is in the range 300-500 for 10,000 grid cells, which corresponds to 40,000 anomalies out of 1 million cells. For DEMs with steps of 20-50 m, there are 30-100 anomalies per 10,000 cells (i.e. 5,000 anomalies per million cells). A new method using tree and sub-tree structures has been developed by the present authors to correct drainage anomalies. However, the details of this method are not discussed further here.
Computation of a monodirectional n-ary drainage tree
After correction of the drainage anomalies, it is then possible to generate a monodirectional drainage tree. Such a tree is defined as the set of all paths followed by the water flowing towards an absolute outlet (at zero elevation) or a relative outlet. In the MNTSURF software developed in our laboratory, the drainage network is handled mathematically as a n-ary tree. Once this tree is calculated, it is stored onto disk along with its n-ary tree structure. As such, this record is a geographical object allowing the introduction of a topology that does not simply cover near-field topology but also incorporates the concept of longer range topology (Wolf 199X; Costa-Cabral and Burges 1994). This is because any given cell of a Digital Elevation Model can be linked topologically to a large number of other cells belonging to the same catchment area, some of which may be located at a considerable distance.
In the example of the Digital Elevation Model with a 500-m step established for catchment basins around the North Sea, the Rhine catchment is composed of 537,621 grid cells that are topologically linked among themselves. The cell containing the outlet is topologically linked to far distant cells lying within the river catchment area of 134,405 km2. The maximum distance between the outlet and a cell situated on the watershed is 1 140.928 km.
2.2. Use of n-ary drainage trees
Visualisation of a drainage tree or sub-tree
Drainage trees or sub-trees may be visualized using the functions associated with the tree structure : by clicking on the mouse, the software application displays the tree or sub-tree of the selected cell and pre-defined colours are used to indicate the path which links this cell with its mother-cell. The display is carried out by search path tree procedure through the drainage sub-tree upstream from the selected cell.
Calculation of the monodirectional surface of a catchment basin
The monodirectional surface associated with the catchment of a grid cell is considered as an attribute of each cell in the Digital Elevation Model. This surface is calculated by tree search path through the monodirectional drainage tree. The monodirectional surface results from the product of the surface of a unit cell and the number of cells obtained by tree search path (Table 1).
Extraction of an estimated hydrographic pattern
Any cell of the DEM is considered to belong to the hydrographic pattern
if the surface of its catchment area is larger than a certain threshold
value. Taking account of the lithologies (shales, sandstones and granites)
and rainfall distribution observed in Brittany, the permanent drainage
pattern is characterized by a very finely divided stream system. To model
this pattern (Seemuller 1989; Meisels et al. 1995), a catchment surface
threshold of the order of 20-25 hectares is considered appropriate for
areas of heavy rainfall in western Brittany (more than 1,000 mm annual
precipitation), while a threshold of about 50-70 hectares is selected for
areas of lower rainfall in eastern Brittany (600-1,000 mm annual precipitation).
The estimated or modelled drainage pattern is a sub-set of the monodirectional
drainage tree, and can show local discrepancies with the real drainage
pattern. Comparisons with the real drainage pattern enable corrections
to be applied to Digital Elevation Models, thus providing a potential avenue
for development and progress in the treatment of DEMs (Fig. 7).
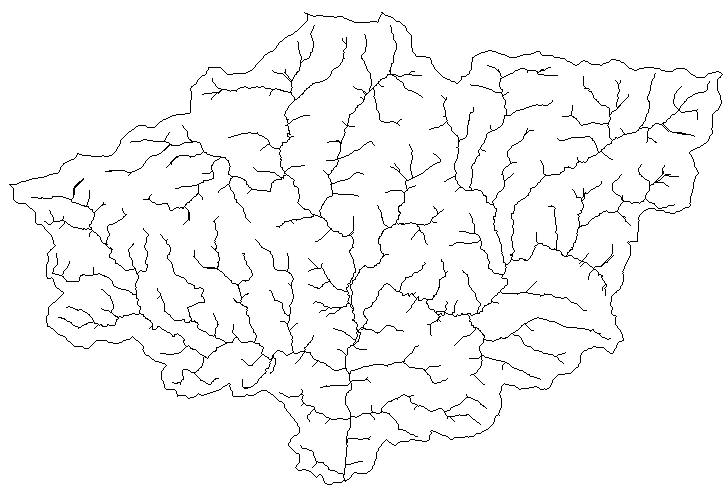
Fig. 7 - Modelling of a drainage pattern by processing DEM data and extraction
of the watershed contours (downgraded DEM with 40-m step, upstream section
of the Aulne river basin).
Figure 7 en 2 dimensions (72k).
Extraction of watershed contours for catchment basins
The identification of DEM cells that lie on the watershed contours of catchment basins is achieved through the tree search path that are adapted for the representation of data using an n-ary monodirectional drainage tree(Fig. 7). Other techniques have been employed to model the watershed contours of catchment basins (Vincent and Soille 1991; Band 1986).
Calculation of the downstream slope
The concept of the downstream slope as proposed by Crave and Gascuel-Odoux
(1996) implies that soil water saturation is controlled by downslope hydrolic
control. It may be assumed that the permanent river system is always occupied
by water, even if the water level undergoes some fluctuation. However,
the water-level fluctuations are of low amplitude, being a few tens of
centimetres in the upstream reaches, while attaining a maximum of a few
metres in downstream reaches or in very large catchments. The downstream
slope is the calculated gradient between each cell of the Digital Elevation
Model and the nearest cell belonging to the drainage pattern (Figs. 8a
and b).
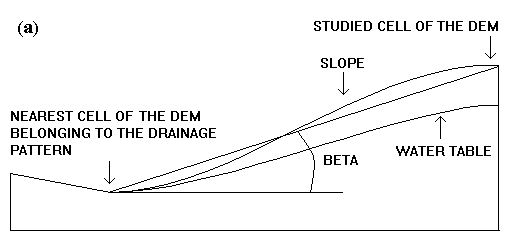
(a) with weak drawdown
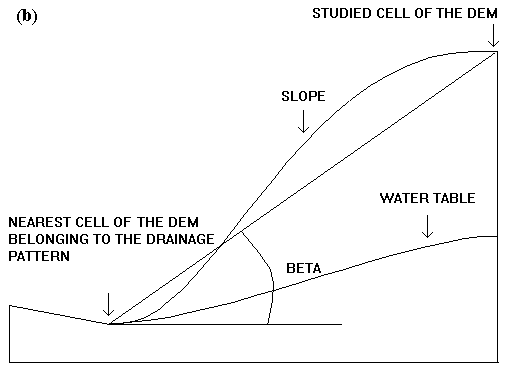
(b) with strong drawdown.
Fig. 8 - Downstream slope
Thus, the downstream slope represents a simple approach to the concept of groundwater level drawdown. In the case of upstream reaches, as soon as the elevation difference between the studied cell and the nearest cell of the drainage pattern is greater than 1-2 m, the error introduced by water-level fluctuations in the drainage pattern becomes negligible.
Tree search path procedure used to process variables imported into the Digital Elevation Model
It may be of interest to use rastering procedure to import values of variables from layers of vector data towards the Digital Elevation Model. Two examples of importation techniques based on rastering procedure are given here :
(1) A layer of data available in vector form represents the net rainfall NR in the studied area. The net rainfall is calculated on the basis of the monthly difference between total precipitation and potential evapotranspiration PET, i.e.: P - PET, when P is greater than PET. From this, we can write:
NR = S (P - PET)
when P > PET
The net rainfall can also be calculated using the monthly actual evapotranspiration AET when P is greater than AET:
NR = S (P - AET)
when P > AET
Using rastering procedure of this data layer, it is possible to obtain the variable NR which is linked to the net rainfall for each grid cell of the Digital Elevation Model. NR corresponds to the net rainfall normalized to the surface area of a unit cell in the Digital Elevation Model.
By tree search path procedure, it is then possible to derive a new variable known as cumulative net rainfall CNR, which is the grand total of net rainfall over the entire catchment for each cell of the DEM. The cumulative net rainfall is an estimate of the mean annual water flux at the outlet of the catchment in river basins that do not possess deep aquifers and/or have mean water residence times of less than one year (Table. 1).
(2) A data layer is available in vector form which describes the nitrogen budget NB for a given region. The nitrogen budget may be calculated from administratively based geographical units using a classical nitrogen apparent mass balance technique :
NB = Nmin + Norg - Ncult
where:
Nmin = nitrogen contributed by mineral fertilisers;
Norg = nitrogen contributed by organic fertilisers;
Ncult = nitrogen consumed by crops.
Similarly as with the preceding case, a rastering procedure of the vector data layer provides a variable known as NB for each cell of the Digital Elevation Model. This variable is the value of the nitrogen budget normalized to the surface of each unit cell of the Digital Elevation Model.
By tree search path procedure, a new variable called CNB (cumulative nitrogen budget) can be derived that corresponds to the grand total of nitrogen budgets over the entire catchment for each cell of the DEM (Quinn et al. 1996). The attribute termed "cumulative nitrogen budget" is an estimate of the annual nitrogen flux at the catchment outlet, in the case where the river basins lack deep aquifers and/or show water residence times of less than one year (Table. 1).
2.3. Construction of a multidirectional drainage model and graph
In a multidirectional drainage model, a given cell of the DEM is assumed
to drain all the water volume from its catchment towards immediately neighbouring
cells at lower elevations (Beven and Kirkby 1979; Holmgren 1994). The volume
of water received by a cell is transmitted to its adjoining cells at lower
elevation, being distributed in proportion to the height difference between
the central cell under consideration and its neighbours(Fig. 9).
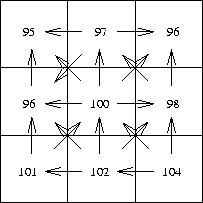
Fig. 9 - Multidirectional drainage model.
Computation of a multidirectional drainage graph
By making use of a multidirectional drainage model, it is possible to generate a multidirectional drainage graph from each absolute or relative outlet. A multidirectional drainage graph has the mathematical structure of a planar graph. In the MNTSURF software developped at the Rennes laboratory, a planar graph structure is implemented in order to handle multidirectional drainage networks in terms of a unique geographical object. Once the network has been computed, it is stored onto disk with its associated planar graph structure. Such a network is a geographical objet which not only allows the introduction of a topology covering the near-field but which also incorporates far-field effects. Any given cell of the Digital Elevation Model can be linked topologically to a large number of cells belonging to the same catchment, some of which may be separated by a considerable distance.
2.4. Use of multidirectional drainage graph
Calculation of multidirectional surfaces for catchments
The multidirectional surface for the catchment of a grid cell is considered
as an attribute of each cell of the Digital Elevation Model. This type
of surface (Beven and Kirkby 1979; Holmgren 1994) is calculated by graph
search path procedure, and corresponds to the product of the surface area
of a unit cell and the number of cells obtained by graph search path procedure(Fig.
10) and (Table 2).

Fig. 10 - Point interrogation of a downgraded DEM (40-m step) covering
the upper catchment of the Aulne.
Calculation of the downslope Beven-Kirkby index
The concept of the downslope Beven-Kirkby index is derived from the Beven-Kirkby index (Beven and Kirkby 1979; Kirkby 1978). The catchment surface used in this case is the multidirectional surface, whereas the gradient corresponds to the downstream slope (Fig. 10). The downslope Beven-Kirkby index combine an upslope hydrologic control of the soil saturation by means of the multidirectional surface with a downslope hydrologic control by means of the downstream slope. It should be pointed out that this index is a topographic or morphological parameter for estimating the importance of water saturated zones and provides good results in the modelling of humid zones, waterlogged low ground or valley bottoms. However, the downslope Beven-Kirkby index is ineffective for the identification of humid or waterlogged zones on high ground, where water saturation is not of topographic origin. In such cases, waterlogging may arise from geological, pedological or textural causes.
Trials carried out by the present authors show that the downslope Beven-Kirkby index is more appropriate than the classical Beven-Kirkby index for estimating waterlogged bottom land. Use of the downslope Beven-Kirkby index makes it necessary to carry out a calibration of catchment areas. For this calibration, a DEM is needed in conjonction with a digitized soil map on a suitable scale (Mérot et al. 1995). For example, a Digital Elevation Model with a 20-m grid step may be combined with a digitized soil map on a scale of 1:25,000 (i.e. carried out with an observation density of one auger sample per five hectares).
Extraction of bottom waterlogged land and contours
The downslope Beven-Kirkby index is a real-number type parameter whose value ranges along a large interval. In order to identify bottom waterlogged land, it is necessary to make use of a calibration which covers a sufficiently wide area and which is based jointly on a Digital Elevation Model and a soil map with reliable information on waterlogging. In western Brittany, we use as a calibration catchment the Kervijen catchment basin (Baie de Douarnenez, western part of France and Brittany). This catchment has a surface area of 5,000 ha and is covered by soil maps on a scale of 1:25,000. Furthermore, a DEM with a grid step of 20 m. is available for this area. For the calibrated Kervijen catchment, we choose a threshold value as to obtain the best estimate of bottom waterlogged soils. Under this condition, the success rate for estimating bottom waterlogged zones on low ground is 80-85% with local over-estimations and local under-estimations. In this field of spatial modelling we intend more to try to minimize over-estimation of bottom waterlogged zones and then to produce a spatial identification of these zones with the highest possible security.
Choosing a threshold value for the downslope Beven-Kirkby index amounts
to producing a binary image based on the presence/absence of waterlogged
conditions on bottom land. The extraction of bottom warterlogged land contours
in raster mode is equivalent to extracting contours from a related connexe
component(Fig. 11).
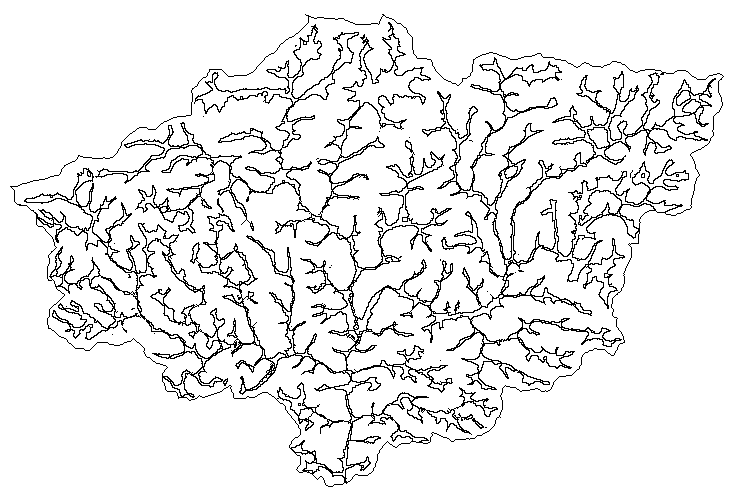
Fig. 11 - Contours of bottom waterlogged zones.
figure 11 zones hydromorphes en 2 dimensions (50k).
figure 11 contours des zones hydromorphes en
2 dimensions (80k).
figure 11 contours des zones hydromorphes en
3 dimensions (90k).
retour au sommaire
3. Studied material
The methods presented above were applied on three different operational scales:
- On a fine scale ranging from 1:25,000 to 1:50,000, based on a DEM with a 20-m step covering the whole of the Brittany region and a lower resolution DEM with a 40-m step derived from the first DEM. The 20-m-step DEM for Brittany (135 million grid cells) was drawn up using two different technologies: stereo-display of SPOT images and ERS radar interferometry. Both DEMs were acquired from the ISTAR company, a subsidiary of SPOT Image. The scale used is suitable for the processing of catchments with surface areas of between 500 and 100,000 hectares.
- On a medium scale of 1:500,000 to 1:900,000, using a 240-m-step DEM downgraded from the previous DEM. This scale is appropriate for regional studies.
- On large scales of 1:1,000,000 to 1:2,000,000, using DEMs with steps of 500 m or 1000 m. To this purpose, use was made of a one minute arc DEM supplied by the USGS covering Europe and North Africa, although it was necessary to modify the geographical projection system and carry out resampling in certain cases. This map scale is suitable for work on very extensive areas such as the catchment basins contributing freshwaters to the North Sea or the southern part of the Mediterranean.
Spatial modelling of bottom waterlogged zones is only possible with DEM with fine grid size (as 20 m, 40 or 50 m). Less detailled DEM with 240 m, 500 m or 1000 m cell size are only suitable for watershed and hydrographic modelling.
4. Results
In view of the methodological approach adopted here, some results are presented from two examples of altimetric databases, one with a grid step of 40 m and the other with 240 m.
The 40-m-step DEM for the north of Aulne catchment (western Brittany), which was obtained from downgrading of the 20-m-step DEM of Brittany, serves as an example of the main functions presented in this study : construction of a monodirectional drainage model and visualization of a drainage tree (Fig. 6), calculation of the monodirectional surface (Table 1), extraction of the estimated drainage pattern (Fig. 7), extraction of watershed contours for the catchment and its sub-areas (fig. 7), calculation of the downslope Beven-Kirkby index and extraction of waterlogged zones located on low ground (Fig. 11).
For the DEM with a step of 240 m covering the Brittany region, results
are given for seven catchments with surface areas greater than 80,000 hectares:
calculation of the monodirectional surface (Table 2), extraction of the
estimated drainage pattern (Fig. 12), extraction of watershed contours
(Fig. 12) and calculation of cumulative (effective) net rainfall as well
as cumulative nitrogen budgets (Table 2).
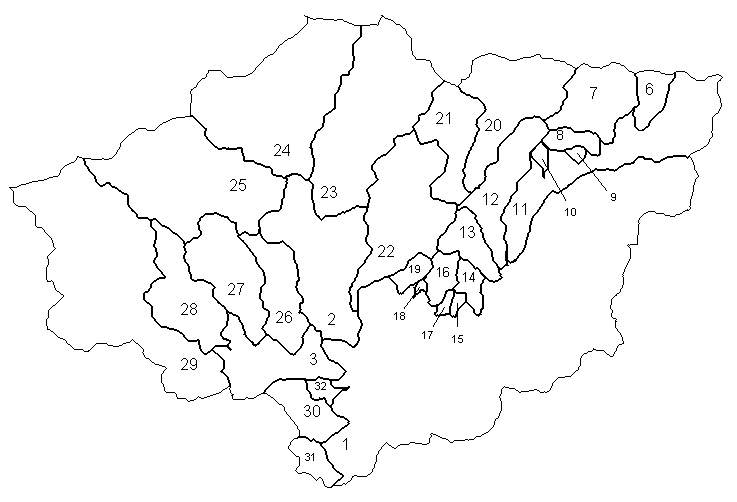
Fig. 12 - Sub-catchments contours in the uptream section of the Aulne river
basin.
figure 12 en 3 dimensions(85k)
retour au sommaire
5. Conclusions
GIS softwares implement topologic procedures that are most of the time near-field or vicinity procedures. Use of tree and graph structures in DEM sotwares allow to introduce long-range topologic properties and allow to calculate several derived variables and to perform some graphic procedures as visualisation of drainage tree or sub-tree.
Figure captions:
Fig. 1 - n-ary tree structure of a natural drainage pattern (example taken from upstream section of the the Aulne river basin, Brittany).
Fig. 2 - Planar graph structure of an artificially modified drainage system (upper Rhine valley, extracted from Digital Chart of the World and imported in a 500 m grid size DEM of western Europe).
Fig. 3 - Example of a monodirectional drainage model.
Fig. 4 - Drainage model (flow vector field).
Fig. 5 - Example of a monodirectional drainage model in the vicinity of a drainage anomaly.
Fig. 6 - A monodirectional drainage network.
Fig. 7 - Modelling of a drainage pattern by processing DEM data and extraction of the watershed contours (downgraded DEM with 40-m step, upstream section of the Aulne river basin).
Fig. 8 - Downstream slope: (a) with weak drawdown;
(b) with strong drawdown.
Fig. 9 - Multidirectional drainage model.
Fig. 10 - Point interrogation of a downgraded DEM (40-m step) covering the upper catchment of the Aulne.
Fig. 11 - Contours of bottom waterlogged zones.
Fig. 12 - Sub-catchments contours in the uptream section of the Aulne river basin.
Table captions:
Table 1 - Database for sub-catchment areas in the upstream section of the Aulne river basin.
Table 2 - Database for catchment areas larger than 80,000 ha in Brittany.
![]()